구조 각관 하중 계산기! (외팔보/양단지지보)

만능 구조 각관 하중 계산기: 상세 계산과정 포함! (외팔보/양단지지보)

안녕하세요! 외팔보 및 양단지지보의 하중 계산, 복잡하게만 느껴지셨나요? 😥 이제 걱정 마세요! 여러분의 구조 설계를 한결 가볍게 만들어 줄 스마트한 구조 각관 하중 계산기와 함께, 핵심 이론 및 상세 계산 과정까지 쉽고 명쾌하게 정리해 드립니다.

본 포스팅에서는 건축, 기계 설계, 혹은 DIY 프로젝트 시 필수적으로 고려해야 하는 보의 응력과 처짐을 손쉽게 계산할 수 있는 웹 계산기를 제공합니다. 더 이상 복잡한 수식에 머리 아파하지 마시고, 간편하게 값을 입력하여 단계별 계산 과정과 최종 결과를 확인해 보세요! 🚀

---

🧐 왜 보의 하중 계산이 중요할까요?

보는 건축물, 다리, 기계 장치 등 다양한 구조물에서 하중을 지지하는 핵심 부재입니다. 보가 외부 힘(하중)을 받을 때 발생하는 내부 저항력(응력)과 변형(처짐)을 정확히 예측하는 것은 구조물의 안전성과 사용성을 확보하는 데 매우 중요합니다.

• 안전성 확보: 허용 응력 및 허용 처짐량을 초과하면 구조물이 파괴되거나 기능을 상실할 수 있습니다.
• 경제적 설계: 과도한 설계를 방지하여 재료비를 절감하고 효율적인 구조를 만들 수 있습니다.
• 사용성 만족: 과도한 처짐은 사용자의 불안감을 유발하거나 다른 부재에 영향을 미칠 수 있습니다.

이 계산기는 특히 구조용 각관(Square Hollow Section, SHS) 또는 직사각형 각관(Rectangular Hollow Section, RHS)을 사용하는 경우에 유용하며, 가장 일반적인 하중 조건인 외팔보와 양단 지지보에 대해 집중하중 또는 등분포하중이 작용할 때의 최대 굽힘 응력과 최대 처짐량을 계산해 줍니다.

---

⚙️ 만능 구조 각관 하중 계산기: 직접 사용해보세요!

아래 계산기에 보의 치수, 재료, 하중 조건을 입력하고 '계산하기' 버튼을 클릭하면, 필요한 모든 값을 한눈에 확인할 수 있습니다. 각 입력 항목에 대한 설명은 다음과 같습니다.

• 하중 유형 선택:
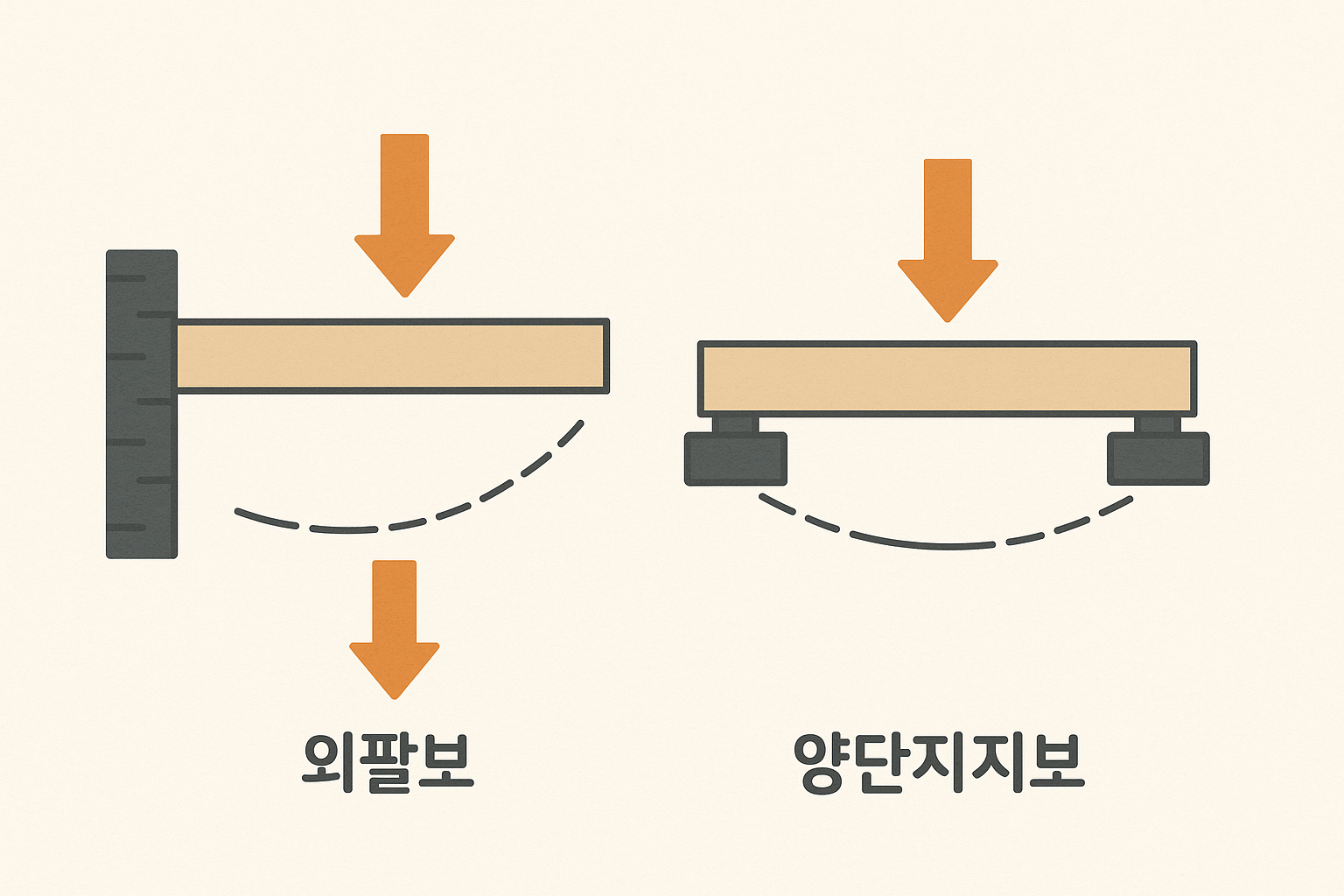
  • 외팔보의 집중하중: 한쪽 끝이 고정되고 다른 쪽 끝단에 하중이 작용하는 경우
  • 외팔보의 등분포하중: 한쪽 끝이 고정되고 보 전체 길이에 걸쳐 균일하게 하중이 작용하는 경우
  • 양단 지지보의 집중하중: 양쪽 끝이 단순 지지되고 중앙 또는 특정 지점에 하중이 작용하는 경우
  • 양단 지지보의 등분포하중: 양쪽 끝이 단순 지지되고 보 전체 길이에 걸쳐 균일하게 하중이 작용하는 경우
• 재료 선택: 일반적인 구조용 강재(SS400), 스테인리스강(SUS304), 알루미늄, 티타늄, 구리의 탄성 계수(Young's Modulus, E) 값을 미리 설정해두었습니다. (GPa 단위)
• 보의 외부 폭 (B, mm): 각관의 외부 폭입니다.
• 보의 외부 높이 (H, mm): 각관의 외부 높이입니다.
• 보의 두께 (t, mm): 각관의 두께입니다.
• 보의 길이 (L, mm): 보의 지점 간 또는 고정단으로부터 하중점까지의 길이입니다.
• 하중 (kg): 보에 작용하는 총 하중의 질량입니다. (계산 시 자동으로 뉴턴(N) 단위로 변환됩니다: \(W = \text{load} \times 9.80665\))

구조각관 하중 계산기 🧮

이 계산기는 다양한 하중 조건에서 구조각관의 응력 및 처짐을 계산하는 데 사용됩니다. 외팔보 및 양단 지지보의 하중 조건을 선택하여, 하중에 따른 구조각관의 성능을 평가할 수 있습니다.

하중 유형 선택: 외팔보의 집중하중 외팔보의 등분포하중 양단 지지보의 집중하중 양단 지지보의 등분포하중

재료 선택 (탄성계수 E): SS400 (205 GPa) SUS304 (193 GPa) 알루미늄 (70 GPa) 티타늄 (110 GPa) 구리 (110 GPa)

보의 외부 폭 (B, mm):

보의 외부 높이 (H, mm):

보의 두께 (t, mm):

보의 길이 (L, mm):

하중 (kg):

계산 결과를 보려면 위 값을 입력하고 '계산하기' 버튼을 눌러주세요.

---

📚 계산에 사용된 핵심 공식들 (이론 맛보기)

이 계산기는 아래와 같은 재료역학의 기본 공식들을 사용하여 결과를 도출합니다. 각 기호의 의미는 다음과 같습니다. (계산기 입력값 기준)

• \(B\): 보의 외부 폭 (mm)
• \(H\): 보의 외부 높이 (mm)
• \(t\): 보의 두께 (mm)
• \(L\): 보의 길이 (mm)
• \(\text{하중 (load)}\): 보에 작용하는 질량 (kg)
• \(W = \text{load} \times 9.80665\): 실제 계산에 사용되는 하중 (N)
• \(w = W/L\): 등분포하중 시 단위 길이당 하중 (N/mm)
• \(E_{\text{GPa}}\): 재료의 탄성 계수 (GPa)
• \(E = E_{\text{GPa}} \times 1000\): 실제 계산에 사용되는 탄성계수 (N/mm² 또는 MPa)

계산 공식 해설 📜

✨ 핵심 포인트! 아래 공식들은 보의 휨(Bending) 현상을 이해하는 데 기본이 되는 것들이에요. 각 공식이 어떤 물리적 의미를 가지는지 살펴보세요!

1. 단면적 (Area, \(A\)): 힘을 받는 재료의 실제 면적입니다.

$$ A = B H - (B - 2t) (H - 2t) \quad (\text{mm}^2) $$

외부 사각형 면적에서 내부 빈 공간의 사각형 면적을 빼서 계산합니다.

2. 단면 2차 모멘트 (Second Moment of Area, \(I_x, I_y\)): 휨에 저항하는 단면의 능력을 나타내는 값입니다. 값이 클수록 휨에 강합니다. \(I_x\)는 x축(보통 강축, H를 높이로 보았을 때)에 대한 값, \(I_y\)는 y축(보통 약축, B를 높이로 보았을 때)에 대한 값입니다.

$$ I_x = \frac{B H^3}{12} - \frac{(B - 2t) (H - 2t)^3}{12} \quad (\text{mm}^4) $$

$$ I_y = \frac{H B^3}{12} - \frac{(H - 2t) (B - 2t)^3}{12} \quad (\text{mm}^4) $$

사각형 단면의 단면 2차 모멘트 공식을 이용하여 전체 사각형에서 내부 빈 사각형 부분을 제외하여 계산합니다. 하중이 주로 작용하는 방향의 단면 2차 모멘트(\(I_x\) 또는 \(I_y\))가 처짐 계산에 사용됩니다. (본 계산기에서는 \(I_x\)를 기준으로 합니다.)

3. 단면 계수 (Section Modulus, \(Z_x, Z_y\)): 휨 응력 계산 시 사용되며, 단면 2차 모멘트를 중립축에서 가장 먼 단면 끝까지의 거리로 나눈 값입니다.

$$ Z_x = \frac{I_x}{H/2} \quad (\text{mm}^3) $$

$$ Z_y = \frac{I_y}{B/2} \quad (\text{mm}^3) $$

단면 계수가 클수록 동일한 굽힘 모멘트에 대해 발생하는 최대 굽힘 응력이 작아집니다.

4. 단면 2차 반지름 (Radius of Gyration, \(r_x, r_y\)): 단주의 좌굴(Buckling)을 검토할 때 사용되는 값으로, 단면의 형상과 관련됩니다.

$$ r_x = \sqrt{\frac{I_x}{A}} \quad (\text{mm}) $$

$$ r_y = \sqrt{\frac{I_y}{A}} \quad (\text{mm}) $$

5. 최대 굽힘 모멘트 (Maximum Bending Moment, \(M_{max}\)): 보가 휘어질 때 단면에 발생하는 최대 회전력입니다. 하중 조건에 따라 다릅니다. (단위: N·mm)

• ✅ 외팔보의 집중하중: \( M_{max} = W L \)
• ✅ 외팔보의 등분포하중: \( M_{max} = \frac{w L^2}{2} \)
• ✅ 양단 지지보의 집중하중 (중앙): \( M_{max} = \frac{W L}{4} \)
• ✅ 양단 지지보의 등분포하중: \( M_{max} = \frac{w L^2}{8} \)

6. 최대 굽힘 응력 (Maximum Bending Stress, \(\sigma_{max}\)): 보가 휠 때 단면에서 발생하는 최대 수직 응력입니다. (단위: N/mm² 또는 MPa)

$$ \sigma_{max} = \frac{M_{max}}{Z_x} $$

이 응력이 재료의 항복 강도 또는 허용 응력보다 작아야 안전합니다.

7. 최대 처짐량 (Maximum Deflection, \(\delta_{max}\)): 하중으로 인해 보가 아래로 휘어지는 최대 변위입니다. (단위: mm)

• ✅ 외팔보의 집중하중: \( \delta_{max} = \frac{W L^3}{3 E I_x} \)
• ✅ 외팔보의 등분포하중: \( \delta_{max} = \frac{w L^4}{8 E I_x} \)
• ✅ 양단 지지보의 집중하중 (중앙): \( \delta_{max} = \frac{W L^3}{48 E I_x} \)
• ✅ 양단 지지보의 등분포하중: \( \delta_{max} = \frac{5 w L^4}{384 E I_x} \)

처짐량은 구조물의 사용성과 기능에 영향을 미치므로 허용 처짐량 이내로 관리해야 합니다.

---

💡 계산기 활용 팁 및 주의사항

• 단위 확인: 모든 입력값은 지정된 단위(mm, kg)를 사용해야 정확한 결과를 얻을 수 있습니다. 결과값의 단위도 확인하세요.
• 강축/약축 고려: 각관의 경우 폭(\(B\))과 높이(\(H\))가 다르면 하중 방향에 따라 강축과 약축이 존재합니다. 본 계산기는 주로 높이(\(H\)) 방향을 휨의 주축(\(I_x\), \(Z_x\))으로 간주하여 계산합니다. 실제 설계 시에는 하중이 작용하는 방향을 정확히 고려해야 합니다.
• 분포하중 입력: 등분포하중의 경우, 전체 하중(kg)을 입력하면 계산기 내부에서 단위 길이당 하중(N/mm)으로 변환하여 계산합니다.
• 단순화된 모델: 이 계산기는 선형 탄성 범위 내에서 거동하는 이상적인 보를 가정합니다. 좌굴, 비틀림, 전단 변형 등 복잡한 현상은 고려되지 않았습니다.
• 안전율: 실제 설계 시에는 계산된 응력과 처짐량에 대해 적절한 안전율(Safety Factor)을 적용해야 합니다. 이 계산기는 안전율을 포함하지 않은 이론적인 값을 제공합니다.
• 전문가 검토: 매우 중요한 구조물이거나 인명/재산에 큰 영향을 미칠 수 있는 설계의 경우, 반드시 구조 전문가의 검토를 받으시길 바랍니다. 이 계산기는 참고용으로만 활용해 주세요.

⚠️ 중요! 본 계산기는 교육 및 참고 목적으로 제공되며, 실제 구조 설계 및 안전 진단의 법적 근거로 활용될 수 없습니다. 중요한 구조물의 설계 및 검토는 반드시 자격을 갖춘 전문가와 상의하세요.

---

🔗 함께 읽으면 좋은 글

롤투롤(Roll-to-Roll) 설비 리와인더(Rewinder)용 파우더 클러치/브레이크 선정 방법

케이블 베어 완벽 가이드 Ver.2: 상세 정보부터 고급 계산기까지

스퍼기어 완벽 정복: 핵심 원리부터 DIY 계산기까지 (모듈, 잇수, 외경, 중심거리)

---

🎉 마무리하며

오늘은 구조 각관의 하중 계산을 도와주는 간편 계산기와 함께 관련 이론 및 상세 계산 과정을 살펴보았습니다. 이 계산기가 여러분의 작업에 조금이나마 도움이 되었기를 바랍니다. 😊 구조 역학은 어렵게 느껴질 수 있지만, 기본적인 원리를 이해하고 이러한 도구를 활용한다면 생각보다 쉽게 접근할 수 있답니다!

혹시 사용하시면서 궁금한 점이나 개선 의견이 있다면 언제든지 댓글로 알려주세요. 여러분의 피드백은 더 좋은 콘텐츠를 만드는 데 큰 힘이 됩니다! 그럼, 오늘도 창의적이고 안전한 설계를 응원합니다! 🚀

구조 각관 계산기, 외팔보 하중 계산, 양단지지보 처짐, 굽힘 응력 계산, 보 설계 프로그램, 구조역학 계산기, DIY 건축 계산, 각관 성능 분석, 티스토리 만능 계산기, 공학용 계산기, 구조 안전성 평가, 재료 강도 계산, 처짐량 예측, 굽힘 모멘트 계산, 단면 2차 모멘트, 단면 계수, 단면 2차 반지름, 탄성 계수, SS400, SUS304, 알루미늄, 티타늄, 구리, 집중하중, 등분포하중, 구조물 안전, 건축 설계 팁, 기계 설계 필수, 구조 엔지니어링, 각관 종류별 강도, 하중 단위 변환, 안전율 적용, 구조 전문가 자문, 계산 과정 상세, 수식 이해, 재료역학 기초, 보의 변형, 구조 계산 오차, 구조 해석 도구, 온라인 계산기 추천, 각관 사용 가이드, DIYer 필수템, 건축 구조 원리, 자가진단 계산기, 정확한 구조 계산, 안전한 설계, 초보자를 위한 구조, 복잡한 계산 쉽게, 공학 지식 공유, 구조 문제 해결, 하중과 응력 관계, 변형과 처짐, 구조 이론 실제 적용, 실생활 구조 계산, 보 강도 계산, 구조 해석 소프트웨어, 건축공학, 기계공학, 토목공학, 구조 계산 웹툴, 무료 구조 계산기, 하중 시뮬레이션, 응력 분산, 재료 선택 가이드, 설계 오류 방지, 구조 계산 튜토리얼, 보 지지 방식, 구조적 안정성, 장기 처짐, 순간 처짐, 허용 응력, 허용 처짐, 구조물 수명, 피로 파괴, 보강 방법, 구조 진단, 구조 유지보수, 하중 조건 변화, 환경 영향 고려, 최적 설계 방법, 비용 효율적 설계, 정밀 구조 계산, 실시간 계산, 즉시 결과 확인, 당신의 구조물은 안전한가요? 1분 만에 확인하세요!, 복잡한 구조 계산? 이제 클릭 한 번으로 끝!, 설계 미스 NO! 정확한 각관 하중 계산 비법 공개!, 처짐 때문에 불안하다면? 이 계산기로 해결하세요!, 초보자도 전문가처럼! 상세 공식까지 알려주는 만능 계산기!, 강성 부족? 파괴 위험? 미리 확인하고 대비하세요!, 당신의 DIY 프로젝트, 이 계산기 없인 시작도 마세요!, 구조 설계의 핵심, 굽힘 응력과 처짐! 이제 직접 계산해 보세요!, 왜 내 보가 휘었을까? 계산 과정으로 원인을 밝혀드립니다!, 안전한 구조물의 시작은 정확한 계산부터!, 지금 바로 테스트하고 구조물의 숨겨진 약점을 찾아보세요!, 놓치면 후회할! 구조 전문가의 비밀 계산 툴 대공개!, 이 계산기 하나면 당신도 구조 마스터!, 더 이상 머리 아플 필요 없다! 보 하중 계산, 이렇게 쉬웠어?, 충격! 이 계산기만 있으면 당신도 구조 엔지니어!, 수억 원짜리 설계 오류, 단돈 0원으로 피하는 법!, 당신의 건물이 무너지지 않도록, 지금 당장 확인하세요!, 구조물 수명 2배 늘리는 계산 비법!, 99%가 모르는 구조 계산의 비밀, 당신만 알아가세요!, 이 계산기 하나로 불안감 ZERO!, 구조 계산, 이제 돈 주고 맡기지 마세요!, 놀라운 정확도! 전문가도 감탄한 각관 계산기!, 미래를 예측하는 구조 계산, 지금 경험하세요!, 당신의 고민을 해결해 줄 궁극의 구조 계산 솔루션!, 계산 오류? 이제 옛말! 완벽한 계산 결과를 경험하세요!, 안전과 효율, 두 마리 토끼를 잡는 방법!, 구조 설계의 판도를 바꿀 혁신적인 계산기!, 이 포스팅 하나로 당신의 구조 지식 레벨업!, 비전문가도 쉽게 이해하는 구조 계산의 모든 것!, 시간 낭비는 그만! 빠르고 정확한 계산으로 생산성 UP!, 당신의 호기심을 자극할 구조 계산의 세계로 초대합니다!, 이 계산기를 사용하지 않으면 손해 보는 이유!, 한 번 사용하면 잊을 수 없는 편리함!, 구조 계산의 새로운 기준을 제시합니다!